Two walls, of heights 5 and 3 units are near each other.
Two ladders reach from the bottom of each of them to the top of the other.
At what height do the ladders cross?

A complete solution to this problem, along with an explanation of how it relates to Shared Work problems can be found here (link updated: 8/12/2022).

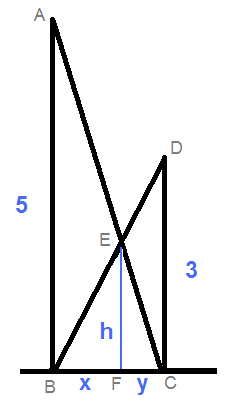Here is a slightly kludgier variation on the solution:


△ABC ~ △EFC => 5 / (x+y) = h/y
△DCB ~ △EFB => 3 / (x+y) = h/x
From those we get 3x = 5y or x/y = 5/3.

Now we venture off the purists' path.

Since it doesn't matter how far apart the walls are (which is true, but not proven here), we arbitrarliy (and conveniently) set them 5 units apart.

That means △ABC and △EFC are isosceles right triangles, with equal legs.

Then x + y = 5, and y = 3/8 * 5 = 15/8 which is also the value of h.

More generally, if the heights of the walls are A and B, then the intersection height is (A * B)/(A + B).

Here is an animated version of the problem, which shows how the height of the intersection point remains fixed as the walls 'close in':