
Visit operators3.html for examples
of operators using swaps of triples instead of pairs.
The way to solve the puzzle with the fewest moves is to
gain some deep understanding of the given permutation.
A more practical way is to solve most of it "by hook or
by crook", and finish with a small unsolved region.
An operator is a sequence of moves. The useful ones
are those that permute a small set of squares, leaving the others
in place when they are done. Typically, operators rotate
three squares (a "triangle") or swap two pairs.
For fastest solving, operators within the largest possible area are best.
But their number quickly explodes.
To keep the numbers under control, we look at operators
confined to a 2x3 region of the grid. There are only 85 of them,
and they are shown below. For a 2x4 region, there are 322, and
for a 3x3 region, 546.
Note that since all moves include horizontally adjacent
pairs, the lines used by these operators need not
be adjacent. They need not align vertically either.
Thus, a "region" can be any collection of sets of 3 (or 4) adjacent
squares, each from a different line.
Operators in 2x3 Region

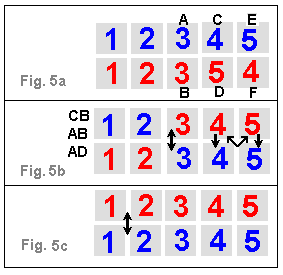
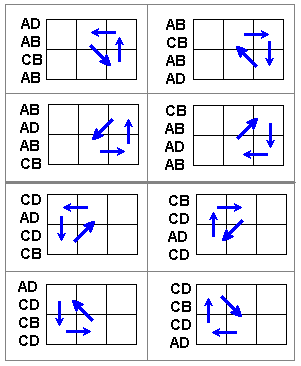
Designate the 6 squares of the chosen region
with the letters A-F (Fig 1).
The notation for moves is as follows:
a letter pair such as AB means
click Card A (selecting A and C), then
click Card B (swapping A & C with B & D).
With 4 moves (Figs 3-4)
we can rotate 3 cards, leaving everything
else the same.
With 6 moves (Fig 2), we can swap TWO
pairs of cards, leaving everything else in place.
Following the sequences shown in each figure
will achieve the result shown: a 3-way rotation
or a two-pair swap.
Because each move swaps TWO pairs (an even number),
it is not possible to swap just ONE pair of cards
with ANY sequence of moves. (See the
Threes page for
the different circumstances when those moves swap three pairs.)
Here is what to do when just a single pair is swapped.
Note that Red 5 and 4 are out of order (Fig 5a).
Apply (CB AB AD) to get 3-4-5 in order for both colors,
but on opposite lines (Fig 5b).
Then swap the 1-2 pairs to get 1-2-3-4-5 on the
two lines, but with colors swapped from the original (Fig 5c).
This was necessary to make the total number of swaps
even, including the one red 5-4 swap.
Catalog of Operators on 3 and 4 cards in 2x3 Region
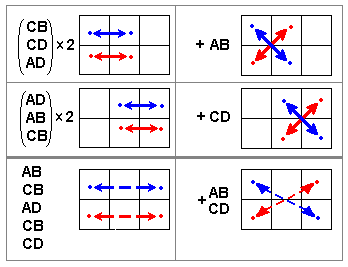
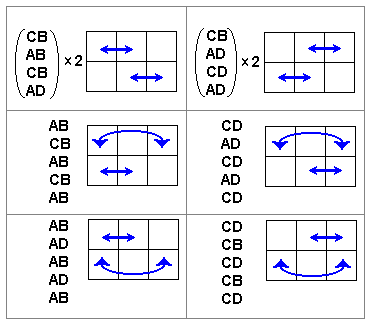
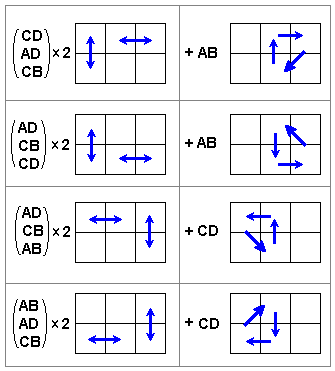
Here is a computer-generated list of all 3-way and double-pair
operators.
| 0. | A C E
B D F | 0 | Start
| | 1. | * * *
D F B | 6 | AD CD AD CD CB AD
|
| 2. | * * *
F B D | 6 | AB AD CB CD AD CD
|
| 3. | * * B
D E * | 6 | AB CD AD CB AB AD
|
| 4. | * * D
E B * | 6 | AD AB CB AD AB CD
|
| 5. | * * B
F * E | 5 | AB AD AB CD CB
|
| 6. | * * F
E * B | 5 | CB AB CD AD AB
|
| 7. | * * D
* F E | 4 | CB AB AD AB
|
| 8. | * * F
* E D | 4 | AB AD AB CB
|
| 9. | * B *
D C * | 5 | AB CB CD AD CD
|
| 10. | * D *
C B * | 5 | AB CD CB CD AD
|
| 11. | * B *
F * C | 6 | CB AB AD CD AD AB
|
| 12. | * F *
C * B | 6 | AB AD CB AB AD CD
|
| 13. | * B C
E * * | 6 | AB AD AB CB CD CB
|
| 14. | * E B
C * * | 6 | AD CD CB AD AB CD
|
| 15. | * D *
* F C | 5 | AB CB AB AD CD
|
| 16. | * F *
* C D | 5 | CB AB AD AB CD
|
| 17. | * D C
* E * | 5 | AD AB CB AB CD
|
| 18. | * E D
* C * | 5 | AB AD AB CB CD
|
| 19. | * E F
* * C | 4 | AD AB CB AB
|
| 20. | * F C
* * E | 4 | AB CB AB AD
|
| 21. | B * *
D A * | 4 | CD CB CD AD
|
| 22. | D * *
A B * | 4 | AD CD CB CD
|
| 23. | B * *
F * A | 5 | AD AB CD CB CD
|
| 24. | F * *
A * B | 5 | CD CB AB CD AD
|
| 25. | B * A
E * * | 5 | CD AD AB CD CB
|
| 26. | E * B
A * * | 5 | CB AB CD AD CD
|
| 27. | B A *
C * * | 4 | CB CD AD CD
|
| 28. | C B *
A * * | 4 | CD AD CD CB
|
| 29. | C D *
* A * | 5 | AB AD CD CB CD
|
| 30. | D A *
* C * | 5 | AB CD AD CD CB
|
| 31. | C E A
* * * | 6 | AD CB AB AD AB AD
|
| 32. | E A C
* * * | 6 | AB AD AB CB AD CD
|
| 33. | C F *
* * A | 6 | AB CD AD CD CB AD
|
| 34. | F A *
* * C | 6 | AD AB AD CD CB CD
|
| 35. | D * *
* F A | 6 | AD CB AB AD AB CD
|
| 36. | F * *
* A D | 6 | AB CB AB AD CD AD
|
| 37. | D * A
* E * | 6 | AB AD CD CB AD CD
|
| 38. | E * D
* A * | 6 | AD AB CB CD CB AB
|
| 39. | E * F
* * A | 5 | AB CB AB CD AD
|
| 40. | F * A
* * E | 5 | AD AB CD CB AB
|
| 41. | C A B
E * * | 3 | CB AB CB
|
| 42. | B E C
A * * | 4 | AD AB CB CD
|
|
|
| 43. | E B A
C * * | 5 | CD AD AB AD CD
|
| 44. | * * B
E F D | 3 | CB CD CB
|
| 45. | * * D
F E B | 5 | AB AD CD AD AB
|
| 46. | * * F
D B E | 4 | AB CB CD AD
|
| 47. | C A D
* E * | 3 | CD AD CD
|
| 48. | D E C
* A * | 3 | AB CB AB
|
| 49. | E D A
* C * | 6 | AB CB AB CD AD CD
|
| 50. | C A *
D B * | 6 | AD CB AB AD CD AD
|
| 51. | B D *
A C * | 3 | CD AB CD
|
| 52. | D B *
C A * | 7 | AB AD CB AB AD CD AD
|
| 53. | C A F
* * E | 4 | AB AD CD CB
|
| 54. | E F A
* * C | 5 | AB CB CD CB AB
|
| 55. | F E C
* * A | 3 | AD CD AD
|
| 56. | B F *
A * C | 5 | AD CD CB CD AD
|
| 57. | C A *
F * B | 5 | AB AD AB AD AB
|
| 58. | F B *
C * A | 7 | AB CD CB AB CB AB CD
|
| 59. | C A *
* F D | 4 | CB AB CD CB
|
| 60. | F D *
* C A | 5 | AD CB AB CD CB
|
| 61. | D F *
* A C | 5 | AB CD AB CD AD
|
| 62. | * B D
C E * | 5 | AB CD AB CD CB
|
| 63. | * D B
E C * | 5 | AD AB CD AD CB
|
| 64. | * E C
D B * | 4 | AD AB CD AD
|
| 65. | * B F
C * E | 5 | CB AB AD AB CB
|
| 66. | * E C
F * B | 5 | CB CD CB CD CB
|
| 67. | * F B
E * C | 7 | AB AD CD AD CD AD AB
|
| 68. | * D F
* C E | 3 | AB CD AB
|
| 69. | * E C
* F D | 6 | AD AB AD CD CB AD
|
| 70. | * F D
* E C | 7 | AD AB AD CD CB AD CD
|
| 71. | B * *
A F D | 4 | CB AB AD CD
|
| 72. | D * *
F A B | 5 | CD CB AB CB CD
|
| 73. | F * *
D B A | 3 | AD AB AD
|
| 74. | * B *
C F D | 3 | AB AD AB
|
| 75. | * D *
F C B | 6 | AB AD AB CD CB CD
|
| 76. | * F *
D B C | 3 | CD CB CD
|
| 77. | B * D
A E * | 5 | CB CD AD CD CB
|
| 78. | D * B
E A * | 7 | AB CD AD AB AD AB CD
|
| 79. | E * A
D B * | 5 | AB CB AB CB AB
|
| 80. | B * F
A * E | 2 | AB CD
|
| 81. | E * A
F * B | 3 | AD CB AD
|
| 82. | F * B
E * A | 5 | AB AD CB AD AB
|
| 83. | D * F
* A E | 5 | AD AB CB AB AD
|
| 84. | E * A
* F D | 5 | AD CD AD CD AD
|
| 85. | F * D
* E A | 7 | AB CB CD CB CD CB AB
|
|








